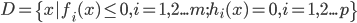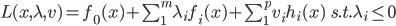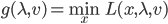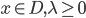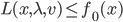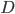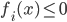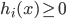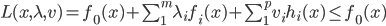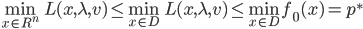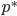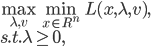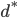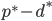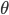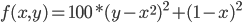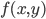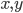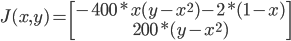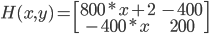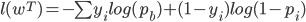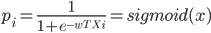优化问题
在regression中通常要对参数求解,通过计算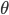 使得loss function最小,或者MLE估计最大,在有函数形式的问题中,通常采用的是牛顿梯度下降法,或者拟牛顿法(BFGS)。下面我介绍下R中如何利用已有函数来求解参数,以及如何手工计算。
使得loss function最小,或者MLE估计最大,在有函数形式的问题中,通常采用的是牛顿梯度下降法,或者拟牛顿法(BFGS)。下面我介绍下R中如何利用已有函数来求解参数,以及如何手工计算。
例1. 目标函数为Rosenbrock Banana function:
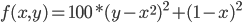
要求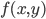 取最小值时的
取最小值时的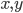 ,即一阶导为0的点,也就是一阶导数的根。方法采用牛顿梯度下降法,需要用到一阶导Jacobian矩阵,和二阶导Hessian矩阵。
,即一阶导为0的点,也就是一阶导数的根。方法采用牛顿梯度下降法,需要用到一阶导Jacobian矩阵,和二阶导Hessian矩阵。
手工计算:
Jacobian matrix: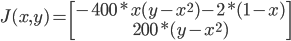
Hessian matrix: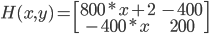
x,y 的迭代公式为:(P249, "Machine Learning: A probability perspective")

R code如下:
fr = function(x) { ## Rosenbrock Banana function
x1 = x[1]
x2 = x[2]
100 * (x2 - x1 * x1)^2 + (1 - x1)^2
}
library(numDeriv)
x = NULL
x0 = c(110,210)
x = rbind(x,x0)
i = 1
for(i in 2:100){
gk = jacobian(fr,x[i-1,])
hk = hessian(fr,x[i-1,])
dk = -solve(hk) %*% t(gk)
xnew = x[i-1,] + t(dk)
x = rbind(x,xnew)
rownames(x)[i] = paste0("x",i-1)
if(abs(sum(x[i,] - x[i-1,])) < 0.00001){
break
}
}
结果如下:
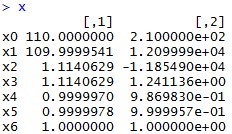
可以看出,从起始点110, 210,通过迭代,到最后1, 1点收敛,说明极值点为(1,1)
optim() in R:
optim(par=c(3,3),fn=fr,method="BFGS")
结果如下:
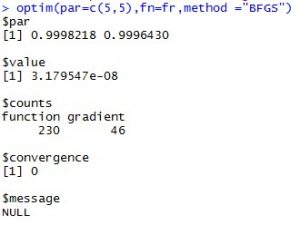
optim中par表示待估参数初始值,fn表示目标函数,method为采用的方法,BFGS为较多使用的,拟牛顿法。注意不同的初始值可能收敛于不同点。
例2. logistics regression
负的MLE函数为: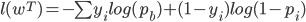
其中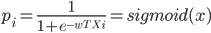
因此我们可以写出目标函数的代码,并且利用optim进行参数优化:
手工计算:
f1 = function(data,w){
p = 1/(1+exp(-w[1] - w[2]* data$gre - w[3]*data$gpa - w[4]*data$rank))
mle = -sum(data$admit * log(p) + (1-data$admit )* log(1-p))
mle
}
f2 = function(data,w){
x = data[,1:3]
y = data[,4]
w = as.matrix(w)
p = 1/(1+exp(-x%*%w))
mle = -sum(y * log(p) + (1-y)* log(1-p))
mle
}
mydata <- read.csv("http://pingax.com/wp-content/uploads/2013/12/data.csv")
m <- as.matrix(mydata)
m <- cbind(rep(1,nrow(m)),m)
optim(par=c(0,0,0),fn=f2,data=m,method="BFGS")
结果如下:
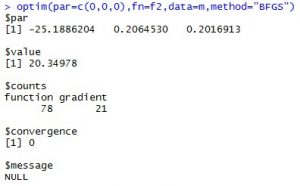
我们用glm logistics regression 来检验:
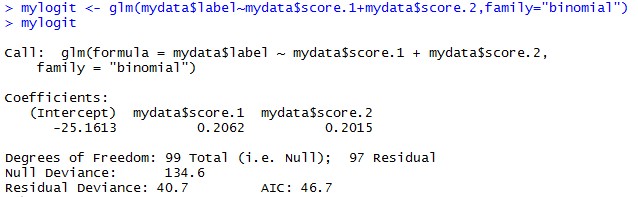
可以看出结果非常接近。
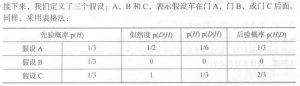
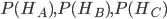 ,那么可知
,那么可知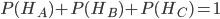 ,另外,由于‘蒙蒂随机打开了门B’是结果事件,因此我们把该结果事件用
,另外,由于‘蒙蒂随机打开了门B’是结果事件,因此我们把该结果事件用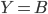 表示,我们设在门A有奖品的条件下蒙蒂打开门B的概率为
表示,我们设在门A有奖品的条件下蒙蒂打开门B的概率为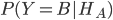 ,同理,在门B或门C有奖品的条件下,蒙蒂打开门B,门C的概率为
,同理,在门B或门C有奖品的条件下,蒙蒂打开门B,门C的概率为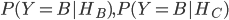 。很显然,在门B后有奖品条件下蒙蒂不可能打开门B,因此
。很显然,在门B后有奖品条件下蒙蒂不可能打开门B,因此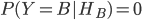 ,那么我们的决策是要求,在蒙蒂打开门B的条件下,门A,门C后面有奖品的概率
,那么我们的决策是要求,在蒙蒂打开门B的条件下,门A,门C后面有奖品的概率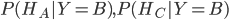 ,很显然,这是一个贝叶斯概率问题,
,很显然,这是一个贝叶斯概率问题,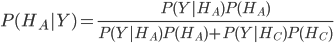
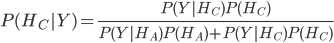
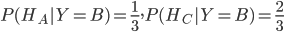 ,由此可以看出,选A和C的概率并不一样。
,由此可以看出,选A和C的概率并不一样。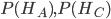 ,确实,这两个是一样概率,但是实际要求得是
,确实,这两个是一样概率,但是实际要求得是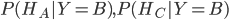 ,而这两个和似然概率
,而这两个和似然概率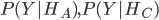 有关,而这两个概率是不一样的。因此在求概率时候,一定要注意条件概率。
有关,而这两个概率是不一样的。因此在求概率时候,一定要注意条件概率。